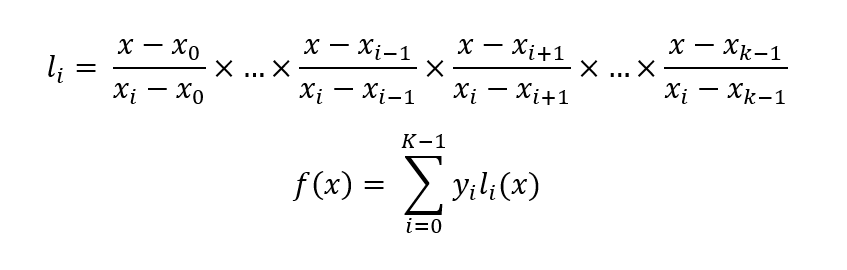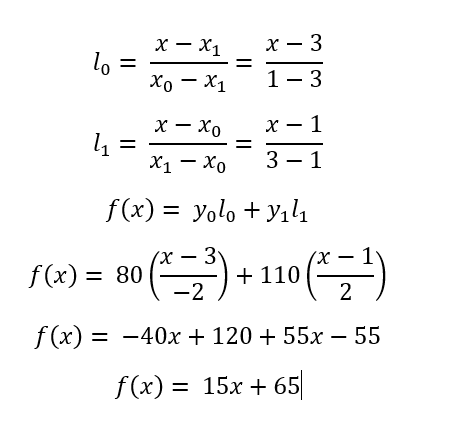[Research] Explain MPC by basic math concepts

Cryptocurrencies have revolutionized the world of finance, offering exciting opportunities for wealth management and transactions. However, security remains a paramount concern in the realm of digital assets. To address this, Multi-Party Computation (MPC) wallets have emerged as a cutting-edge solution, leveraging the power of basic math to enhance security while managing cryptocurrency funds.

---

Understanding the Basics of MPC Wallets

At its core, an MPC wallet is a cryptographic innovation that enables multiple parties to collaboratively manage and transact with cryptocurrencies while maintaining the privacy of their individual inputs. Let’s delve into this concept using fundamental math principles.

Imagine a scenario where Alice is new to cryptocurrency. She’s worried that if she forgets her private key, she could lose all of her crypto assets. She reaches out to her friends, and they’re willing to help her protect her key. Traditionally, Alice might share a single private key, which is a risky approach. However, with MPC wallets, she can embrace a concept known as “secret sharing.”

Secret Sharing

Alice’s intention is simply to have her friends assist her in case she loses her private key. With MPC, Alice will “split her private key into N parts.” Let’s say Alice’s private key is S=65. She wants N=4 friends to help secure her funds, and ONLY if she receives at least K=2 (where K <= N) approvals, she can recover the key.

1. Initially, in order to encrypt the secret code, Alice build a polynomial of degree (K – 1).
2. Therefore, let the polynomial be y = a + bx. Here, the constant part ‘a’ is her private key (S)
3. Let b be any random number, say b = 15.
4. Therefore, for this polynomial y = 65 + 15x, she generates N points from it
5. Let those 4 points be (1, 80), (2, 95), (3, 110), (4, 125). Clearly, she can generate the initial polynomial from any two of these 4 points and in the resulting polynomial, the constant term a is the required secret code

Alice sends each part of the key to her friends, and now she can use her wallet without the fear of losing her private key.

Recover private key: The Art of Mathematics

One day, Alice discovers that she has lost her private key. She can reach out to at least 2 of her 4 friends to reconstruct her private key. The following equations illustrate how they can compute it:

For example Alice collected 2 points (1, 80) and (3, 110) from her friend. She can employ Lagrange basis Polynomial to construct the private key, The Lagrange basic Polynomial say:

Let reconstruct the private key with given 2 points:

• Now the private key is 65

Remember that, ONLY if Alice has the approval from at least K=2 friends, she can reconstruct the key

Real-World Applications and Beyond Basic Math

In real-world MPC wallets, advanced cryptographic protocols and algorithms are employed to ensure the highest levels of security. The use of sophisticated mathematical techniques safeguards transactions against various types of attacks, including collusion attacks and insider threats.

MPC wallets also open the door to exciting possibilities, such as decentralized finance (DeFi) applications, where multiple parties can pool their assets for lending, borrowing, and yield farming while maintaining control over their private keys.